各位老师,大家上午好,很高兴又和大家一起在元卓学堂探讨关于人工智能,特别是关于深度学习的算法的一些理解,以及学习的一些体会吧。 那么我今天就接着大概三个月前的一个话题,因为中间安排了一些其他的事情,也是我这边因为事情比较多,所以就停了一段时间,我们今天接着前面的神经网络的背景,继续介绍关于卷积神经网络。
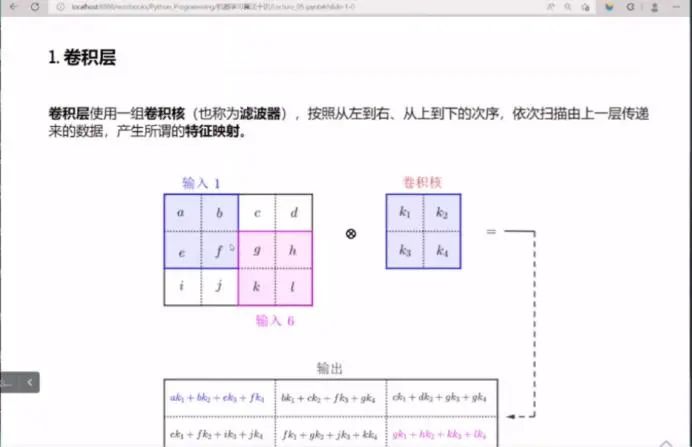
我们都知道卷积神经网络是现代人工智能,就是所谓的新一代人工智能复兴的核心要素之一,卷积神经网络虽然并不是所有部分都是原创的,但是它确实是引入了很多新的思想。具体来讲,在以往的神经网络的这种基本的架构之上,引入了这样几个最重要的思想,第一个就是卷积层。对于卷积层,实际上我们一会儿分析的时候就可以看到,它实际上是我们原来经典的神经网络连接的一种局部化,也就是说我们原来的那个神经网络,它的一层和下一层,它的连接是所谓的全连接,也就是说每一个神经元都要跟下一层的每一个神经元都要有连接,这样的话,由于这种指数效应,组合爆炸问题,像这种经典的传统的神经网络,它不可能连接的层数太多,因为太多的话都是乘的关系,所以它就像我们要学习的参数一样成指数的增加。积神经网络它实际上从某种程度上化简了这种连接,它基于人的神经网络工作的基本原理,一个神经元它只跟它周边的若干个神经元相联系,并不是说跟所有的神经元都相连,那么他把这种思路用到卷积神经网络中,就是其一,提取出其中比较适合于视觉视神经这个相连的这种思路,构造了这个卷积层,这是一个新思想。那么第二个新思想就是池化,池化其实也可以看成是一种局部化的一种基本方式,但是它局部化的方式跟卷积层的方式不太一样,一会儿我们可以看到它的一些特点。第三个重要因素就是在卷积神经网络里面,它引入了若干个新的这个激活函数,从而彻底释放了做激活函数计算这一步的它的潜力,那么传统上我们经典的神经网络,通常都使用s 型函数,s 型函数虽然在数学上很完美,但是它也有众多的问题,其中最重要,最主要的一个问题就是它的计算,虽然数学上计算性能很好,但是它的计算复杂度会很高,那么在卷积神经网络具体实施的时候s 型函数它往往占了很重的计算负担,所以引入了很多便于计算的一些函数。像 Re l LU,整流线性单元,像双曲正切函数,像softmax 等等,这些函数的计算负载并不比tanh低,像后面这两个,但是我们有大量可以高速运行的,就是它实施方面的一些措施,可以减轻绝对准确的这种计算,所以新的激活函数,它取值范围的灵活性,也为输出结果,也不一定解释为概率值,那这样的话也为不同类型的任务开辟了一个新的思路。 好,这是卷积神经网络在传统的神经网络基础上引入的三种新思想,当然还有很多,那么我我们觉得这三类可能是最核心最基本的。 前边其实在讲神经网络的时候,关于激活函数我们已经说了很多,所以我们这一讲就不再去讨论激活函数,只去关注卷积层和池化层。卷积层的基本思想我们通过这个图来看一下。实际上对所有维度的数据都有对应的卷积操作,但通常我们用的比较多的就是这种二维数据,就是这种表格型数据,二维数据,所以我们会把输入数据写成一个矩阵的形式,就是矩阵平面二维的数据形式,然后对应的卷积核也是二维的,有一个二维数据,然后有一个卷积核,那么这卷积核就像拿一个放大镜一样,那么根据卷积核的大小,依次的扫描输入数据,在扫描过程中,它的次序是从左到右,从上到下,也就是先扫描左上角,然后依次向右移动,一直移动到最后把它全覆盖,然后再往下移,接着再覆盖下边,这里边会有技术上的一些细节,比如说你向右移动的时候,每次移几个单元,每次移几步,这叫步长。然后向下移的时候,同样也有一个步长,也就是每次向下移动多少个数据的位置,这些细节我就都不去考虑它了,因为它就是一些加减乘除比较琐碎的计算,本质上不影响我们的变换结果,然后他具体的计算方法,像加权,求和,和经典神经网络加权求和的方法就非常类似了,也就是用卷积核里面每个值依次去和它所盖住的,也就是当前正在扫描的这一段数据的相应位置的值相乘,然后相加,所以我们淡蓝色的这一部分做卷积,它的结果就是用这个值a 乘k 1,然后加上b 乘k 2,加上1乘k 3,再加上1 乘k 4,就是这个值,那么这就是新输出位置上的一个值。然后他接着往右移动,现在假定说我们是步长为1,所以就往右移动一个单位,就用b 乘k 1,然后c 乘k 2,f 乘k 3,g 乘k 4,以此类推,再往上移一位就是c 乘k 1这一项,这时候到头了,所以再往下一个移位就到了这一部分,那么这一部分就是ek1 一直到g k 4,所以它的移动次序就是从左向右,到头以后返回到开始,然后往下移,再从左到右,那么按照运行次序依次扫描,直到卷积核把所有的输入数据全部都覆盖住,产生的输出也排成二维数表的这种格式,我们可以看到这个卷积操作,刚才我说过它实际上就是我们原来那个经典神经网络加权求和这种方式的一种局部化,也就是说它每次操作的时候,都和他里边的一小块做加权求和,我们把卷积核的这个值看成是权重,这个是原始数据,所以它就是一个加权求和。因此在卷积神经网络里面,我们模型的参数实际上就是这些卷积核的里边的具体的数值,这具体的数值跟经典神经网络的情况实际上是类似的,因为我们知道经典的神经网络,它的学习参数实际上就是加权求和里边的权重,因此卷积核里面的数值实际上就起到局部位置上的一个权重的含义。由于卷积核的尺寸相对来讲,跟输入数据相比,它会比较小,所以这样的话,我们的权重数,具体到一个卷积核上来讲,这个权重的数就会比较少,所以你可以有多个卷积核,而且用不同的卷积核来产生不同的效果,这就是我们下面说的它的局部性,这是刚才那个例子的具体计算,我们拿这个作为一个具体计算的场景来示例一下,其实这个计算过程非常简单了,假如说它的原始图像就是这样一个蓝色的阵列,是5乘5的,那么这个深蓝色部分就表示这块有一个图形,比如说一个数字7,然后这个深色的部分表示它是1,假如说我们先处理的是黑白图像,是纯粹的黑白图像,所以只用两个位就可以了,就是0和1,那么这个深色的就是1,这周边就是0,任意数值的时候其实道理是一样的,我的卷积核是一个2乘2的窗口的卷积核,就是两个像素单位,两个数据单位用这个卷积核,这是卷积核就是001,所以我们把它区分开, 1的地方是深色,0的地方就空下来,那么我覆盖这个位置的时候,它的形状是这样子的,所以这两个做卷积的结果就是把它们逐位相乘,这是逐位相乘的结果,也只有这个地方是1,所以跟它乘出来的是1,其他位置全是0,然后把这四个位置的值相加,逐位相乘的是加权,作为卷积核的值,作为权值和原始数据进行相乘,对应的位置相乘,然后把它们加起来,用求和符号去求和。然后向右移,又移到这儿,那么这个位置是001,所以再和这个地方相加,相依次相乘相加,所以这两个有1的位置都对应的1,然后把它们相加,相加之和就是2,以此类推,比如说我这个灰度,灰度值就是说它如果是一个一个层级的话,那2就比它要深一点,依次类推。卷积神经网络之所以重要,不仅仅是因为它引入了加权和的这种思想,更重要的是,如果我们把这种加权和计算进行广义的理解,那么实际上后来大量的新模型,实际上都类似于这种卷积操作,只不过计算不是完整的加权求和过程,也可能是别的方式,比如说一会我们要讲到的池化层,它实际上也是一种计算,只不过它不是用加权求和,后来的很多发展都会发现类似的操作,那么这个卷积计算的过程,不要把它简单理解成加权求和这样的常规性操作,比如说我用一个一般操作来代替的话,那么它就会产生各种各样的其他类型的模型,这就是卷积操作的原理。具体的计算过程我们就不再细说了,刚才已经都讲过了。 下面我们再看池化层,池化层至少在表述上比卷积层会更简单一些,原因就是他运算的部分比卷积层要简单。
先看池化层怎么操作,然后再返回来。池化层,为什么还称为子采样或者亚采样 ?池化有很多办法,最常用的办法就是所谓的最大池化Max Pooling。顾名思义,最大池化就是我们取池化窗口覆盖的那组数据中最大的那个值,我们看这个例子,假如说这个是原始图像总的数据,这个绿色的就是池化窗口,那么也就是它覆盖多少个数据点。现在我覆盖四个数据点,2乘2的窗口,那么在这四个数据点中,显然5是最大的对吧?所以我把5选出,池化操作完了以后向右移,同样这个时候也有个步长,向右移几个格子,池化一般我们不去做重叠部分,所以我向右移的时候,实际上是移动两个格子,是两个单位,所以这个时候的池化的步长是2,跟刚才那个卷积操作的1是有点差别的,所以我向右移动就盖住这一部分,那么这一部分最大值是6,所以把6保持下来,向下移到这儿,最大值是7,把7保留下来,然后再向右,最大值是8,把8保留下来,池化窗口在原始数据上依次也是从左向右,从上到下这样一个次序来移动,然后他会把每次移动盖住的那组数据中最大的选出来,构成新的数据,所以我们可以看到池化的两个特点,一个特点是池化有点类似于我们把窗口盖住的这些数据扔到一个池子里面,然后从中挑选最具代表性的,这就是池化含义,因此池化有多种方法,你不一定非得取最大池化,也可以取说平均,比如我取这四个值的平均值,那么这就是平均池化。当然也可以取其中最小的,或者是其他某些规则确定的那种值。在卷积神经网络应用中,最常用的还是最大池化,很少使用别的,当然这也是我们针对不同应用得到的经验,这是第一个特点。第二个特点,如果你的池化窗口是2乘2的,那么相当于每次把四个数据点缩成一个,这样对于二维数据而言,相当于池化的结果会把原来数据的大小减少一半,比如说这里原来是4乘4的, 那么池化一圈以后,这个数据会减半,变成了2乘2,所以你可以认为池化实际上是浓缩原来数据中最重要的那些值,比如最大值,所以说通常都是最明显最重要的一些值,同时减少了数据量,数据量减半,这是池化映射的特点。那么就像刚才说的,我们可以看到它的另一个特点就是它的运算,实际上跟卷积核的运算是有相似之处的,也就是它的次序,从左向右,局部运算的性质,是跟卷积层非常类似的,只不过它不是用的,加权求和,所以池化窗口里边没有参数,不用去训练,不用去学习,这样的话,实际上我们的池化过程的计算会比卷积层的计算更简单,也更快速,同时减少了数据量,虽然减少数据量但它还保留了原始数据信息,比如说图像的话,就是原始图像的很多重要的信息,数据原始图像中值是最大的,那么在不同的情况下往往就代表着它最显著。无论是卷积操作还是池化操作,性质上它都是在提取原始数据中的某些特征,比如说图像的特征,语音数据的特征,因此卷积和池化这两个操作通常也叫做特征映射。在卷积神经网络这个领域里,当说特征映射的时候,它实际上是有两层含义的,或者指的是卷积层,它的运算从原始数据到结果的这样一种映射,也可以指的是池化,从原始数据到池化后结果的一个映射。这一些用法在卷积和池化是通用的。当然还有一部分是激活函数,通常激活函数它不是用在卷积层或者是池化层,而是用在跟随在卷积层和池化层后边的线性层,也就是传统神经网络的连接,然后输出一个类似于概率的东西,或者是输出一个可以通过值的大小来衡量它到底是归属在哪一类,这样的一个标志性的一个数。激活函数本质上来讲,它是属于经典神经网络的一部分,所以我们这里就不再去花时间讲激活函数了,它直观的含义也比较明显,差别就在具体的公式,所以下面我们就转向实际操作,看看我给的五项任务以后,然后根据完成这项任务设计一种模型,然后通过这个模型来实现对原始任务的解决。那么我们下面通过一个非常著名的卷积结构叫做LeNet,然后通过PyTorch 来实现,我们问题的背景就是CIFAR10的数据集,一会儿我再解释这个相应的过程。这个是LeNet的构造,因为CIFAR10等待的原始解决的问题是CIFAR100,这个比例比较复杂,那CIFAR10是后来经过简化的一个数据集,有一些小图像来进行分类用于教学,那么LeNet 的结构就是这样一个结构,在这个结构里它实际上是跟这个任务相关联的,首先,这个CIFAR10就是图像数据库,它的数据都是32乘32点阵的,32个像素乘32个像素,所以图不是很清楚,都是模模糊糊的,大家可以看到这个图,是一个青蛙的图,非常的模糊,因为它经过放大,32乘32它肯定不会那么大,真正的大小大概也就这个里面的白色框框那么大,而且它是彩色的,所以它有三个通道,r g b 三个通道,那么LeNet 实际上就是专门为这个图像而设计的,所以它的结构就这样,我们大致过一下这种结构,第一个它要过一个卷积层,因为有三个通道,所以每个通道都要对应的不同的卷积核,为了让这个图像的特征能够提取的更明显,所以第一个特征映射就是卷积层的特征映射,它的输入当然就是它的尺寸,这个图像的输出,就是28乘28,也就是说输出会缩小,然后根据32乘32,要把它缩成28乘28,然后再根据卷积核指定卷积核的大小,调整步长,就是每次移动多少,然后还要调整填充,就是这个图像,如果你移动到边缘的时候,不能保证它被卷积核所全部覆盖,这个时候你就要在四周进行填充,这些都是一些技术细节,虽然很麻烦,但是从道理上来讲他其实不重要,最前面这个6就表示它有第三个维度,是六维,二十八乘二维,平面的,实际上还有第三个维度,就是这三个通道,每个通道各有一幅r g b 。然后下一个就是池化层,池化层用的是2乘2池化,所以这个原来28乘28图像变成14乘14,过了池化层以后,再经过卷积的特征名称,变成10乘10,同样这个也是要有一定的变化模式。那么配套是把这些东西都掌控好了,所以我们就不用去花时间去计算,我们究竟应该有多大的填充,有多大的补偿这种问题。下一个是第二组池化层,10乘10,现在变成了5乘5,然后第三个维度变成6,这个它会根据需要自动调整池化层的所有输入,那么作为完整的输入数据,把它拉成一个一维的数据,然后进到一个线性层,全连接层,这就是标准的神经网络层,然后再进行一个输出,这是十个神经元的,那这十个神经元就对应十种不同的图像,也就是看你这个位置,十个输出的位置,哪一个位置最大,就说明你最有可能是这一类里边的一员,这是它的标准结构,其实看起来复杂,但是因为PyTorch已经隐藏了大多数的这种计算的细节,所以我们很容易 在PyTorch 里边把这些参数直接传给它就可以,不用去关注这里面的细节,那么这个人大家都知道它是一个法国人,他给自己起了一个中文名字叫杨丽昆,他最近出了一本书叫做《科学之路》,这本书非常值得一读,希望对人工神经网络,特别是卷积神经网络发展历史和发展过程有兴趣的老师可以去翻一翻这本书,有很多启发,也就是说我们今天在中小学里边去谈论人工智能,恐怕谈论的不仅仅是一些技术,我们更多的要看一看用什么手段进行了突破,在突破的时候他的思路是什么,以及当时所遇到的种种障碍,目前我看到的杨丽昆这本书写的是最生动活泼的,也是最使得普通人能够看到人工智能发展历程的非常有个性的一本书。大家也都知道,杨丽昆在二零一九年和卷积神经网络的另一位主要发明者,还有另一位,三个人一块得到了二零一九年年度图灵奖,所以推荐给大家读一下《科学之路》。然后我们我们回到这儿,这个CIFAR10是因为它已经被广泛的用于人工智能模型的教学,所以它已经成为P y T o r c h 的内建数据集,所以使用的时候用标准的导入数据方式就可以,CIFAR10它只有十个类别,标签是0到9,所以跟手写体字母识别的数据集有点类似,稍微复杂一点的就是它是彩色图,但是分辨率很低,因此每幅图是三个颜色通道和32乘32像素,那么这个图是官方的一个示例图,也就是从中选出十副,属于某一类的,这里边我们可以看到这10类是飞机、汽车、鸟、猫、鹿、狗、青蛙、马、船和卡车,原始的数据集有一百个种类,那么现在拓展的更多,甚至上千,这样的这个数据集,所以它的难度会越来越大,然后我们使用PyTorch是来做一个基于LeNet 的卷积神经网络的分类器,就是对图像进行分类这样的一个模型。首先我们先加载数据,加载数据前面已经用过了,所以这就不多解释了,第二步我们要定义这个LeNet,它的网络架构跟以前一样,我们定义一个类,这个类就是把网络架构完整的定义出来,它的每一层,它的输入,输出相应的一些参数怎么去界定,这是第二步。那么第三步,我要选择一个损失函数,选择一个优化器,然后我们定义在学习过程中,如何来搜集损失函数的值,比如说他要做多少次,每次是怎么做的等等这些信息,然后我们根据定义好的模型,根据加载好的数据集,分好的训练集和测试集来做训练,用训练集训练,然后用测试集测试,这是一个标准的流程。我们大家还对第四讲有印象的话,那么我们可以对照一下第四讲,它实际上和第四讲的流程几乎是一模一样的,我们先导入库,因为这个例子有一些地方运行起来还是要有点时间的,所以我为了节省时间,就不在我的讲座过程中直接运行了,这个实际上是可以直接运行的,那么有兴趣的老师可以代码开出来的,然后在到相应的环境里边去自己跑一遍,一般用稍微好一点的这个机器,运行最后的一个程序,时间大概是五分钟左右,不会太久,它毕竟还是简化的一个版本。这段代码我们把训练集来导入,可以看到跟我们以前搞那个magic 的数据集的时候几乎是一样的,只不过在这后边换了一个名字而已,就是它内建数据集的名字,然后我们可以做一下数据集的基本考察,这个我也不做了,也就是看一看他出的一些图像,那么在对数据集进行检验和考察的过程中,它里边会有一些编程上的细节,这个主要是因为我们开始也遇到过这个问题,就是那PyTorch张量,他在存储数据的时候,把数据存储的格式跟把图像转成Numpy数组的时候是不一样的,它这个中间次序不一样,也就是PyTorch 是按照颜色通道,高度和宽度来存储的,而Numpy的图像是高度宽度颜色来存储,所以使用不同的函数的时候,那编程的过程中,所以你需要用一个函数,这个permute 有置换,要把它这几个轴来进行置换,而且这个置换如果只是一次换两个轴的话,你要换两步,那把这放到最后再做一次,那么我们可以看到置换的那个函数,就是用在这儿,所以在读代码的时候,你知道这个图像数据以后就更加容易,因为原始的训练集数据是PyTorch格式的是吧,然后这个数据要经过轴的置换,就把表示图像不同维度的那个轴换成这个Numpy显示图像这个函数,就是mutplotlib 这个函数的格式显示成这样,然后我们还需要进行图像的这种所谓的归一化,其实这个相当于把图像每个像素点的取值范围放到一个特定的值范围,因为原始图像是取值域是(0,1],取这些(0,1],它并不对应着每一个r g b 通道,标准的就是0~255这样的像素,每个图像颜色深浅度,所以(0,1]把它变换成[-1,1],这个主要是在计算的过程中要用这样的一个范围,这是它变换的过程,我就不再多解释了,那么这一段代码是做变换的,变换完了以后我们分别把训练集和测试集,来加以分离,那CIFAR10大概有六万幅图像,其中有五万幅就用来训练的,有一万幅是用来测试的,那么我们把训练集和测试集分别装到这个测试集、训练集和测试集里面,也是相当于装在我们的工作环境里,然后把每个类做一个中文标记,其实这都是一些准备工作,准备前面的数据集,其实这个最好的办法就是大家下去把它完整的运行一遍,为了你能看的清楚,所以我把所有的变量都是用中文写的,这个地方不要出错,一个字出错那就可能导致整个程序运行不成功。好,那么下面最关键一步就是构建我们LeNet的一个结构,我们使用这个n n 模块,就是PyTorch这里的神经网络的一个模块,来定义一个类,这个类就是我们LeNet模型,所以我现在用的这种办法是最简单的办法,但是它不是最好的办法,那么我们用PyTorch的话,通常就是用这样一个模块,可能会比这个更简单一些,这个定义方法它的好处就是我们可以清楚的看到,它和刚才那个LeNet 系统模型结构图能够对应起来,前面这不用讲了,这都是定义,这个就是在n n 模块里面定义模型的必备的一些步骤,所以这里开始。那么在这个卷积层里面,后面这些参数,那么大家可以去跟图里面去对比,其中有一个值是窗口,就是卷积核的大小,这个5乘5卷积核的大小,其他的我们在里边都可以看到,这个3相当于是输入里边的三个维度,相当于输出就是卷积核的层,记得黄色那个层是六层,然后这个5是卷积核的大小,有了这三个参数以后,它会自动匹配,比如说我用多长的步长,用多大的边缘去填充,它会自动匹配这个。这个是池化层,池化层就简单了,你只需要指定哪个是池化层的大小和步长,大小就是2乘2 ,步长也是,每次既然是2乘2,就每次移动一个完整的池化的隔层,所以也是2。下面是第二个卷积层,也是com 就是卷积层函数的二维表示,是二维卷积层, 刚才我们讲到那个卷积,理论上来讲,它适合于任何维度,也就是说它既适合于一维数据,也适合二维数据,也适合于三维等更高维度的数据,那么它的这个含义跟刚才也一样,就是我们上一个输入第三个维度是6,然后我们要产生于第三个维度为十六的,这样的一个就是卷积层,然后卷积核的大小仍然是5乘5。这个地方可以看出来是我们是三个关键层,第一池化层,第二卷积层,那么值得注意的就是我们还有一个卷积层没有写,那一个卷积层是放到了我们前向传播计算损失函数值的时候再使用,然后是三个连续的线性层,这是输入,一共有16个,第三维度是16,然后二维维度的大小是5乘5,所以它的总的数据量是他们的成绩,然后是一个一百二十个神经元的全连接层,所以这个是输入,这一个线性层的时候是一百二十个神经元,所以这个参数是一百二十,然后下一个就是线性层,那么输入当然就是一百二十,它输出还八十四个,就是很容易做到的,然后再下一个是八十四到十,我们回过头来再去看LeNet的结构图的时候跟这一对,那么这些参数的含义就一目了然了, 由这儿我们也可以看出来为什么这个例子它具有典型性,我们只要把这些值设成一个变量值,那么这里面有一些值是直接由上一个继承下来的,比如说像这个到这一步,它不好去直接指定你的输入到底是多少,但是你可以根据它前一个参数值去把它乘出来就可以了,是吧?所以这样的话假如说我要用一个变量,然后把这个变量作为它里面的参数来传递进去,那么就很方便了。所以这个例子就是为了简单,我们实际上是就做了一个the night 原始的结构,这是定义它的创建模型那部分,然后这个类里边有了模型,那你还要定义,这个模型里的数据是如何向前面传递的,就是forward ,这个传递的方式,第一卷积层作用一下ReLU这里面的函数,它是在神经网络的里面有一个functional,那个里边有各种各样的功能性函数,所以这个案例中,在第一卷一层要做一次,你看做了一次最大值化,在这儿定义了一个最大值,因为它两次最大值都是一样的,都是2乘2的,所以你看这个地方只是定义了池化的结构,真正让池化起作用的实际上是做了两次,做了两次就是第一次做了卷积以后经过ReLU 激活函数,然后再做池化,第二次再做第二卷积层,然后再做池化,就刚才我说,但是池化作用在向前传播的时候才起作用。在这儿只是一个构造,它只是定义构造并没有说它在哪个位置, 这个地方就做了位置,然后第一卷积层激活池化,第二卷积层激活池化,这不就相当于前两个卷积池化那个层的这个数据,先过这两个,都做完了以后,我们把这数据拉成一个一维数据 ,就是最后的维度是这么大就这个,-1就表示我拉成一维数据,那么你到底有多少个就自动计算,然后经过第一个线性层,这是第一个线性层,对吧?经过第一个线性层以后做一次ReLU,然后再过第二个线性层,再做一次ReLU,然后再过第三个线性的,所以第三个线性层我们在看结构图的时候,可以看出来它写的是高度连接,所谓高度连接就是它直接用全连接,不再作用激活函数了,为什么不再作用激活函数了 ?这主要是因为你在输出之前就再做一次这个激活函数,实际上就是产生输出了,就产生0~9某个最大值了,所以一旦产生误差的时候,那么我们就要在它最后一次激活函数输出之前,通过这个误差值去往前回溯,也就往前这个梯度下降,那么在这个回复过程中,最后一次计算实际上是多余的,也就是说我们反正也要反过去,最后一次激活计算实际上是在运行阶段做,一会儿我们看这个运行阶段的代码可以了,这样的话我定义这一类以后,创建网络的一个实例。那么创建这个实例以后,所有这些参数也就都给你定下来了, 一个类就相当于一个小区,我的房子都是一样的,就是一个设计师设计的,所以你创建一个实例,就是你要到这个具体的位置去找一栋,比如说第几行,第几列的某一栋某一楼层的某一间,也就是挑一个具体的,这样人为的参数,我们不需要学习和训练的这些参数就已经确定下来了,所以整个的卷积神经网络,其实最核心的就是这一步,跟LeNet那个图做一个对比我们就可以看到,为什么PyTorch 在最近几年做深度学习,做人工智能会广受广受欢迎,就是他的这种建模能力非常的强也非常直观,这个还是比较比较麻烦的,如果简单的话,我们还可以把这整个的都包到一条语句里面来.然后选损失函数,那么现在是多元分类,所以我们用多元交叉熵,这个就不细说了,然后再指定学习算法,那么通常都是梯度下降了,为了改善梯度下降法的性能 ,通常加上一点随机性,然后再加上一个动量参数,直观的理解就好像我拿一个球,在山坡上一个高度,我把这球放到山坡上,让它往下滚到最低点,那么这个球它不是真空中存在的,它是有重量的对吧?它是有初始速度的,所以这个动量参数实际上你可以理解成这个球的初始速度和它的重量是这样的一个标志,所以它是模拟的一个物理,大家知道这个球越重 ,那么它下降落速度就快 ,但是也带来一个问题 ,就是你太重的话,它遇到一个小坑的时候会跳不出去 。所以它是模拟那个物理场景,就给予这样一个参数,以达到做梯度下降的时候最好的办法,这就是指定交叉熵损失函数,然后这一条指令算法就是优化算法,就是SGD 随机梯度下降,然后里面参数非常的简单。学习率,这个我们在讲一般神经网络的时候已经讲过了,学习率就是我们在做建模过程中,在具体训练之前做的最后一步。下面我们就开始进行训练,这个我这里面选的是我轮两次,也就把所有的训练集的数据我跑两遍,然后每一批跑两千,所以这样的话我们就可以把这个训练过程按批次,它的损失函数值的这种降低能够直观的看出来,这就是训练的这个代码, 那么我们可以看到它的整个结构是非常简单的,那么我看一下它的大致结构,首先一个外循环,这二就表示我在整个数据集上跑2次,叫做两轮,官方用语就是epoch ,就是轮次。当然你如果要想达到更好的效果,这个要大一点,那比如说一百,通常是选一百,如果要是一百的话,那么普通的计算机大概要跑两个小时左右,所以这个要谨慎一点,如果你没时间跑的话,就简单一点,当然这个训练数太少,结果不会太好,然后这个损失值累积在整个训练集里边来做一个循环,那他跑遍这个零就是说我们选训练集里边不要标签的部分 ,这是获取数据,把学习过程中梯度下降计算先清零,然后我们用反向传播优化这三步, 先输入数据,然后计算输出数据跟实际标签,因为它都在循环里面,所以最后产生结果就是个总和, backward 就是反向传播,这个就是每一次用优化算法一步一步,每循环一次优化一次,每循环一次优化一次,然后计算统计值,这个也可以,明显的看出来就是我每两千显示一次,过两千用两千除一次,所以过两千以后它就会重新计数,然后把这个累加值除以一个两千,那这样的话 ,就等于是我每两千里的累加值全循环完了以后就产生结果, 真正需要时间的是这个代码会运行时间比较久。好,那么剩下的这些就是看测试了,你就选一组图片,然后用测试集里的图片去测一测它预测的实际效果,那最后我们可以写一个短的代码去把整个的正确率,也就是把图像进行分类的正确率显示出来,如果训练的次数足够的话,就是你的批次足够,大概训练十次以上吧,那么准确率可以达到百分之七十几,如果两次的话,大概只有百分之五十五左右 ,所以会比较低一些,但是这已经够高的了,就是说百分之七十几的已经够高了,因为你猜准的那个就是瞎猜,所以每个图像的准确率只有百分之十左右,那么经过适当的训练,可以达到百分之七十五,加大数据集的这个量里边的一些改善程度,那么LeNet最后就是用这种结构对CIFAR10的这个训练准确度提高到百分之八十五左右,但是到八十五以上就很难了,你还可以写一段代码去看一看对哪类图像判断的准,哪类图像判断的不准,我觉得这个例子里面的代码,它的好处就是它和我们的直观联系的非常紧密,而里面编程技巧性的东西,又可以说压缩到了最少,那么这样的话就非常便于我们把思想转换成代码这样实际的转换过程,也便于我们做实验,唯一不好的地方是你还有定量,所以真正训练起来是比较耗时的,那么这就是我今天跟大家一起分享的第五讲,关于卷积神经网络,谢谢大家的收看,我们下次再见。
